How insurance companies can be a force for responsible climate policy
What insurance company would even think of offering flood insurance for Mar-a-Lago?

(Mark Hulbert, an author and longtime investment columnist, is the founder of the Hulbert Financial Digest; his Hulbert Ratings audits investment newsletter returns.)
CHAPEL HILL, N.C. (Callaway Climate Insights) — By 2050, President Trump’s Mar-a-Lago Florida resort is projected to be under at least a foot of water for 210 days per year.
What insurance company would even think of offering flood insurance for that resort? If this projection is even close to being accurate, Mar-a-Lago will become uninsurable at some point in the next 30 years.
And what is true for it will soon become true for much of southern Florida. In fact, it may already be true. Because of King Tides — especially high tides caused by gravitational pulls from the sun and moon — so-called sunny-day flooding has now become routine in some parts of Miami. When that happens, salt water can seep up through the city’s drains and, mixed with sewage, flood the streets.
According to the Washington Post, you aren’t able to get a long-term mortgage in some parts of Miami.
Normally I’m not inclined to feel sorry for insurance companies. But assessing the economic impact of potential weather disasters was already hard enough before climate change entered the equation. So I don’t envy the challenges they will face in coming decades. Many companies that insure against weather disasters will go out of business, either from poorly-priced bets that lose big, or from deciding that the uncertainty is too great to build a sound business model upon.
To get a sense of the magnitude of this uncertainty, consider hurricane risk — perhaps the biggest of the weather-related disasters that insurance companies currently insure against. According to reinsurance company Swiss Re, total U.S. hurricane losses over the past five calendar years (through 2019) amounted to close to $300 billion, or an average of around $60 billion per year. Over the first five years of the 1980s, in contrast, the comparable total (in 2019 dollars) was less than $25 billion, or about $5 billion per year.
That certainly seems like a significant difference. But that appearance may be a function of insufficient data. The presence or absence of a single category 5 hurricane will have an outsized influence on these totals — making it extremely difficult to detect a trend. In fact, according to an article in the Bulletin of the American Meteorological Association that focused on the period from 1900 to 2017, there actually is no long-term trend in the number of major hurricanes making landfall in the continental U.S.
No trend
Continental U.S. landfalling major hurricanes by year from 1900 to 2017
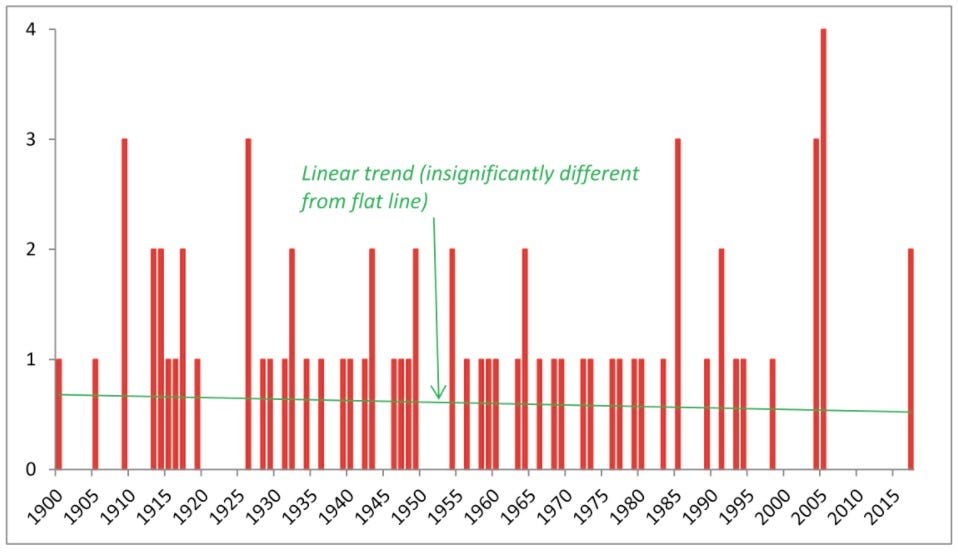
Source: Bulletin of the American Meteorological Association, July 2018.
It is, of course, distinctly possible that a long-term uptrend doesn’t show up in the data because climate change has accelerated only recently, and that after the passage of several more decades we could more accurately predict how climate change will affect the frequency and severity of hurricanes. But for insurance policies written now, companies can’t wait.
Furthermore, according to Adam Sobel, a Professor of Applied Physics and Applied Mathematics and of Earth and Environmental Sciences at Columbia University, “we lack theory on how hurricane frequency will change as the climate warms. We do not even have a good understanding of what controls the overall number of [hurricanes] presently.” (Sobel was quoted in a Swiss Re publication earlier this year titled Natural catastrophes in times of economic accumulation and climate change.)
Sobel added: “Historically, numerical simulations have tended to show that [hurricane] frequency declines with warming, but in the past few years some advanced models have instead produced increases. If storms produce stronger winds, heavier rains and more coastal flooding [as some models predict], but the total number of storms declines, the total hazard — the probability of an event of given magnitude at any given location — might remain constant or even fall. But if the number of storms increases, and so too does the intensity of accompanying wind and rainfall, the risk posed would be much higher.”
Sobel concluded: “This results in large uncertainties in the overall assessment of hurricane risk.”
Indeed.
Regardless, we shouldn’t be overdeveloping coastal regions
There is one aspect of hurricane risk about which there is little uncertainty, however: Over-development in low-lying coastal areas greatly magnifies the economic losses caused by hurricanes. Independent of what is happening with the climate, major hurricanes that occur today cause a lot more damage than those of yesteryear because more people live in areas affected by hurricanes, and property values in those areas are much higher.
Swiss Re recently tried to estimate the economic damage that would be caused if a hurricane with identical track and intensity to the 1992 Hurricane Andrew were to hit south Florida today: “Accounting for increased asset exposures, we estimate the original economic loss amount of $23 billion would be $80 billion to $100 billion today.”
This is why it’s so important that the trend towards overdevelopment in low-lying coastal regions be reversed. Ironically, insurance companies may be a catalyst towards this happening. If hurricane insurance rates in south Florida get too high, or insurance companies withdraw from that market altogether, then development could come to a halt quickly.
Who would have thought that insurance companies might be a force for progress on the environment?
In this regard, it will be important that the federal government not intervene to make it possible for over-development to continue even after private insurance companies start pricing themselves out of the market. If that happens, of course, the taxpayer inevitably would end up footing the bill for cities foolishly trying to fight climate change.
If taxpayer dollars are to be spent responding to the potential of flooding in low-lying coastal areas, they should be used to incentivize people to move to higher ground.

